ECOLE POLYTECHNIQUE DE LOUVAIN

SHOCKLEY-QUEISSER EFFICIENCY LIMIT.
INTRODUCTION
Efficiency is one of the most useful parameters to compare solar cells with each other. Over the years, more precisely in the 50s, many scientific articles were written in order to prove a maximum limit of efficiency a solar cell based on Si. In 1960, Shockley and Queisser published their paper : "Detailed Balance Limit of Efficiency of p-n Junction Solar Cells" which was a major breakthrough in the scientific community.


In their article, Shockley and Queisser mention a concept called "ultimate efficiency". It is a theoretical upper limit of efficiency in solar cells, also called detailed balance limit. Indeed, before Shockley and Queisser wrote their article, there were already predictions of efficiency vs energy gap curves in the literature.
However, they were based on certain empirical values, etc. which wasn’t theoretically justifiable. Shockley and Queisser claimed there was an theoretical justifiable upper limit based on basic physical laws, more precisely the concept of detailed balance. This upper limit was called detailed balance limit, but is also known as the ultimate efficiency. The previously calculated efficiencies (renamed semi-empirical limit by S&Q) and the new upper limit are compared in the figure on the right. This new upper limit offers new confidence in achieving much greater efficiencies
than previously thought.
This efficiency limit is an essential concept for solar panels, it expresses the maximum amount of electricity that could be potentially produced with incident solar energy. Knowing the Shockley-Queisser limit helps engineers understand which bandgaps (and thus, which materials) are good candidates in designing high efficiency cells. Note that this limit only applies to single p-n junctions. Hence, multi-junction cells are able to overcome this limit, unlike the latter.
WHY DOES THE EFFICIENCY HAVE A BELL SHAPE?
Before beginning the calculations, it can be interesting to analyze why the efficiency follows the trend as seen in the previous figure. Indeed, it reaches a maximum for a certain bandgap and then, the efficiency becomes very small for both small and big values of bandgaps, why is that?
It can be quite intuitive to understand why the efficiency is low for larger values of the bandgap. Indeed, if the bandgap is too big, only photons of high energy will be able to absorb. This leads to a decreasing efficiency because it directly limits the amount of photons that will be able to absorb into the cell to produce electricity.
On the other hand, if the bandgap is small, a much larger spectrum photons will be able to absorb, which could make us think that the efficiency will be the largest for the smallest possible bandgap. However, if the energy of the photon is much larger than the bandgap of the material, it will lead to inevitable losses of energy in the form of heat. Indeed, no matter how high the energy of the photon is, only one electron can be freed by its absorption. Hence, these losses in the form of heat lead to lower efficiencies. Moreover, with smaller bandgaps, the electrons and holes can recombine more easily than with larger ones. This recombination mechanism can also lead to a loss of efficiency
MODELS CONSIDERED
For this analysis of the Shockley-Queisser limit, we will consider 4 models :
1.
An ideal spherical solar cell irradiated by a black body sun
2.
A flat solar cell irradiated by a black body sun
3.
A flat black body solar cell irradiated by a black body sun
4.
A flat black body solar cell irradiated by the actual solar spectrum
1 - EFFICIENCY OF AN IDEAL SOLAR CELL

The calculation of S&Q’s maximum efficiency first begins with an ideal solar cell. The latter is spherical, which means it will receive radiations from all directions. Additionally, it is hypothesised that no radiation is emitted from the cell (Tc = 0K).
The cell is subjected to a black body radiation (the Sun) which is at 6000K. Moreover, it will be considered that photons with energy greater than hνg will have the same result than photons of energy of exactly hνg. On the other hand, photons of energy lower than hνg will produce no effect.
Figure 26 : Schematic representation of the solar battery considered : a spherical solar battery surrounded by a black body of temperature Ts. The solar battery is at temperature Tc=0K.
assumptions of the first model
One Sun
We consider the light intensity of one sun.
Carriers
The carriers have infinite mobility to diffuse to the contacts
Sun blackbody
The Sun is a blackbody at a temperature of Ts = 6000K
Spherical cell
The cell is perfectly spherical, receiving radiations from all around it and emitting no radiation itself (Tc = 0K).
THEORY
The efficiency can be calculated with this general relationship :

From this, we need to find an expression for both Qs and Ps. Qs is the amount of photons having a frequency greater than νg per unit time and area for a given black body radiation of temperature Ts. In other words, Qs corresponds to the amount of photons absorbed per unit time and area for Ts. From well known formulas, we have that :

Ps corresponds to the total energy density per unit time and area for a blackbody radiation of temperature Ts. Once again, its expression is given by well known formulas :

Now that we have expressions for Qs and Ps, the maximum efficiency of a singular p-n junction solar cell can be calculated as a function of the energy gap. Note that xg = Eg/kTs

ULTIMATE EFFICIENCY OF AN IDEAL CELL

Figure 27: Ultimate efficiency u(xg) as a function of the energy gap Eg of the semiconductor
The maximum efficiency for an ideal solar cell is approximately 43.8 %, which corresponds to an energy gap of 1.1 eV. This corresponds to the properties of silicon.
In the case of our perovskite (MAPI), which has a bandgap of 1.57 eV in the tetragonal form according to literature, we observe a maximum of approximately 39.6 %, which is lower than silicon.
Cubic MAPI, with a bandgap of 1.61 eV, has a slightly lower efficiency of approximately 38.7% and finally, orthorhombic MAPI has the lowest efficiency of all with a value of 36.84 %.
All of these values are assembled in Tab. 8. However, these results correspond to an ideal cell. A more realistic vision would need to consider a cell of planar shape emitting radiation with a certain angle of incident radiation coming from the Sun. These will be considered in the following models.

Table 8: Ultimate efficiencies of Si, orthorhombic MAPI, cubic MAPI and tetragonal MAPI from Shockley-Queisser theory in the case of an ideal solar cell.
2 - EFFICIENCY OF A FLAT SOLAR CELL

A second and better approximation of the efficiency is done by assuming a flat cell with the the Sun as a point source. The cell is illustrated in the figure on the left with Tc = 0 K (the cell does not emit radiation).
The incident radiation hits the solar cell with a specific angle, therefore, the cell does not receive radiation from all directions
Figure 29 : Schematic representation of the solar battery considered : a planar cell irradiated by a spherical sun subtending a solid angle ωs at an angle of incidence θ
assumptions of the SECOND model
One Sun
We consider the light intensity of one sun.
Carriers
The carriers have infinite mobility to diffuse to the contacts
Sun blackbody
The Sun is a blackbody at a temperature of Ts = 6000K
Flat cell
The cell is perfectly flat, receiving radiations radiation from an incident angle θ and emitting no radiation itself (Tc = 0K).
THEORY
To consider the influence of this incident angle, we consider that the ultimate efficiency is affected by a factor cos(θ) such that we have :

ULTIMATE EFFICIENCY OF A FLAT CELL

When the light is normal to the cell (0◦), the efficiency is maximal, which is to be expected. The more deviated the incident light becomes, the more
the efficiency decreases, until eventually reaching 0% at θ = 90◦
Figure 28: Ultimate efficiency u(xg) as a function of the incident angle for silicon, tetragonal MAPI, cubic MAPI and orthorhombic MAPI
From these results, we understand how important the angle of incidence is when using a solar cell.
In order to have the best possible efficiency, this angle should always be optimized. To do so, several techniques are possible.
Firstly, solar panels are mounted with a certain tilt angle. As the position of the Sun in relation to Earth changes during seasons, the tilt angle can be adapted during the year in order to optimize the efficiency. Moreover, it is essential to consider where on Earth the solar cell is placed. Depending on whether the cell is located near the equator or not, the tilt angle will have to be modified.
Solar tracking systems can also be used to adjust the angle of cell in order to always make it face the sun with an optimal incidence angle. This way, the panel is able to capture the maximum amount of sunlight during the day and have a a much as possible consistent efficiency.
3 - EFFICIENCY OF A BLACK BODY FLAT SOLAR CELL

Figure 29: Schematic representation of the solar battery considered : a planar cell irradiated by a spherical sun subtending a solid angle ωs at an angle of incidence θ
Compared to the previous scenario, we will now consider that the cell acts as a black body with Tc = 300K (ambient temperature). Hence, the cell now emits radiation as well.
The cell is now assumed to be a black body, this means that radiative recombination process is now possible. In general, two types of recombination can be defined : non-radiative and radiative recombinations. Non-radiative recombinations is a process in which free electrons and holes recombine
and energy is lost as heat. This affects the efficiency of the cells negatively because less charges are able to contribute to the current.
Radiative recombination is the inverse of photon absorption : an electron goes from the conduction band to the valence band to recombine with a hole by emitting a photon. This photon can then be absorbed in the cell and converted into current, thus affecting the efficiency of the cell positively.
assumptions of the third model
One Sun
We consider the light intensity of one sun.
Carriers
The carriers have infinite mobility to diffuse to the contacts
Cell blackbody
The cell is flat and a blackbody at a temperature of Tc = 300K.
Sun blackbody
The Sun is a blackbody at a temperature of Ts = 6000K
Recombination
The only recombination mechanism is radiative recombination
Incident light
The sun is a point source. The incident radiation hits the solar cell with a specific angle.
THEORY
The efficiency can be calculated with this final relationship :

(1)
where u(xg) is the ultimate efficiency as calculated before, v is the ratio of open-circuit voltage Vop to ultimate voltage Vg and m is the impedance matching factor, which is a ratio between the maximal power and nominal power.
The efficiency η depends on several variables, which we define as the following :
xg
It represents the following ratio : xg = E/kTs
xc
It is the ratio between the temperature of the two blackbodies : xc = Tc/Ts
ts
It is the probability that a phonon with energy hv>Eg incident on the surface produces an electron-hole air for the sun blackbody.
We assume ts = 1 in order to reach the balance efficiency limit
f
f = fcfωts/(2tc) where fω is a geometrical factor that depends on both the solid angle subtended
by the sun ωs and the angle of incidence on the cell θ, tc is the probability that a phonon with
hν>Eg incident on the surface produces an electron-hole pair for the solar cell blackbody and fc is the fraction of radiative recombination
In order to get to this final result, a thorough discussion must be lead. Firstly, to calculate the efficiency, we consider that :

where we used Watt’s law to calculate the maximum output power of the solar cell.
Calculating the incident power is trivial :

(2)
where fω is a geometrical factor defined earlier. A is the area of the body.
Then, we need to calculate the maximum output power for the numerator of Eq. 1. It is obtained when the product I*V is maximal. In our specific case scenario, the current-voltage relationship is the following :
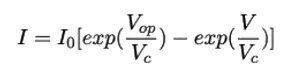
where Voc is the open-circuit voltage, Vc is the voltage of the cell.
The maximum is reached when d(IV )/dV = 0, hence the maximal power is obtained when :

We can introduce the impedance matching factor m, which compares the maximum power to the nominal power IshVop

with zm = V(max)/Vc
(3)
The nominal efficiency can be expressed in terms of Vop, the open-circuit voltage (I=0) and Ish, the short circuit current (V=0). For a planar cell of projected area Ap, the short circuit current is IP = qApfωtsQs. By using both this relation and Eq. 2, we can obtain :

(4)
By replacing the first member of Eq. (3) in Eq. (1), we obtain

Finally, by replacing Eq. (4) in the previous relation, we have :

Hence, we have proven the previously given expression for calculating the efficiency of a one-junction planar cell irradiated by a spherical sun subtending a solid angle ωs at angle incidence of θ
ULTIMATE EFFICIENCY OF A BLACKBODY PLANAR CELL

The results obtained in this section are more realistic than the results obtained in the
ideal cell section.
The various curves represent the efficiency for different values of f. The efficiency decreases with decreasing values of f.
Figure 30 : Efficiency η for a blackbody solar cell at Tc=300 K, with sun at Ts=6000 K as a function of the bandgap Eg for different values of parameter f
We can also plot the efficiency curve for perfectly absorbing cell (ts = tc = 1) with normal incidence
(fω = ωsπ = 2.18 · 10^(−5)) and no nonradiative recombination (fc = 1). This corresponds
to f = 1.09 · 10^(−5). We can observe that compared to the figure of efficiency of an ideal cell, silicon and tetragonal MAPI perovskite now share similar values of efficiency.
Among the 3 phases that MAPI can take form in, orthorhombic MAPI has the lowest efficiency. The value of these efficiencies are assembled in the table below

Figure 31 : Efficiency η for a blackbody solar cell at Tc=300 K, with sun at Ts=6000 K as a function of the bandgap Eg for a perfectly absorbing cell (f = 1.09 ∗ 10^(−5) ). The respective efficiencies of orthorhombic MAPI, tetragonal MAPI, cubic MAPI and silicon are shown on the plot.

Table 9: Ultimate efficiencies of Si, orthorhombic MAPI, cubic MAPI, tetragonal MAPI from Shockley-Queisser theory in the case of a perfectly absorbing flat solar cell
4 - EFFICIENCY OF FLAT BLACK BODY CELL IRRADIATED BY THE ACTUAL SOLAR SPECTRUM

Figure 32: Spectral irradiances of a black body with the temperature 5900 K (yellow), the solar radiation at the outer edge of the earth’s atmosphere (extraterrestrial sunlight, orange) and at sea level (terrestrial sunlight, rainbow-coloured). The spectral irradiance is the power in watts of radiation incident on one square metre of surface area. The surface is defined to be fixed perpendicular to the sun. The terrestrial sunlight spectrum corresponds to a cloudless day, the sun is at an angle of 48.19° towards the zenith and blue sky radiation is ignored.[40]
In this section, we study the effect of using the real solar radiation spectrum at sea level instead of using
the approximation of the sun as blackbody. On Fig. 32, we can observe the true solar spectrum at different levels : extraterrestrial sunlight corresponds to the actual spectrum of the sun before entering Earth’s atmosphere and terrestrial sunlight corresponds to the remnants of the solar spectrum that are able reach the surface of the sea after going through our atmosphere. In the previous models, we had considered the Sun to be a black body of approximately 6000K, this corresponds to the yellow curve on Fig. 32. However, in reality, this is not the actual spectrum that will be able to reach our solar cell. Indeed, instead, we should consider the terrestrial sunlight spectrum.
It is interesting to note that the solar spectrum is different in space than on Earth at sea level due to our atmosphere. When sunlight goes through the atmosphere, a process known atmospheric attenuation occurs. In other words, some portion of wavelengths of light are scattered or absorbed by aerosols, hydrometeors (condensed water particles) or gases constituting Earth’s atmosphere [41]. Using the data from NREL AM1.5G spectrum [42], we have the solar radiation spectrum at sea level in Fig. 33. Using this spectrum instead of the blackbody approximation should lead to efficiencies closer to reality.
The main reasoning in this section was extracted from the GitHub repository from S.Byrnes [43]
assumptions of the fourth model
One Sun
We consider the light intensity of one sun.
Carriers
The carriers have infinite mobility to diffuse to the contacts
Cell blackbody
The cell is flat and a blackbody at a temperature of Tc = 300K.
Sun real spectrum
The Sun spectrum at sea-level is taken into account
Recombination
The only recombination mechanism is radiative recombination
Incident light
The sun is a point source. The incident radiation hits the solar cell with a specific angle.
THEORY

Figure 33: Real solar radiation spectrum at sea level using data from NREL
Using the data from NREL AM1.5G spectrum [42], we have the solar radiation spectrum at sea level in Fig. 33. Using this spectrum instead of the blackbody approximation should lead to efficiencies closer to reality.
The main reasoning in this section was extracted from the GitHub repository from S.Byrnes [43]
The main difference in the computation of the efficiency for this model compared to the previous one is Qs, the number of photons of energy greater than Eg per unit area per unit time.
In order to compute a new expression of Qs, the first step is to convert the solar radiation spectrum units from NREL. We can hence define the amount of solar photons per unit time, per unit photon energy-range,
per unit area of the solar cell :
From the previous expression, we can obtain Qs by integrating it from Eg to Emax. Qs is plotted
in Fig. 34.

Figure 34: Total number of solar photons with energy above the band gap, per unit time, per unit ground area on earth
Following this, we can apply the same reasoning as for the previous model. We find the ideal short-circuit current and ideal open-circuit voltage as a function of bandgap. From there, the Shockley-Queisser limit is found in Fig. 35

Figure 35: Efficiency η for a blackbody solar cell at Tc=300 K, using the solar spectrum at sea-level.
In conclusion, by using the actual solar spectrum at sea level, we should be obtaining more realistic efficiencies η. Silicon still achieves the best efficiency with η = 33%. However, MAPI also achieves quite high efficiencies. This is one of the reasons why MAPI perovskite is such a serious contender in research for use in future solar panels

Table 10: Ultimate efficiencies of Si, orthorhombic MAPI, cubic MAPI, tetragonal MAPI when considering the real solar radiation spectrum with Shockey-Queisser theory
Overcoming the Shockley-Queisser effeciency limit
As mentioned earlier, the Shockley-Queisser efficiency is an upper theoretical limit for singular p-n
junctions. In reality however, there are many ways to reach higher efficiencies in our solar cells. Firstly, the Shockley-Queisser limit only concerns singular p-n junctions. To reach higher limits, we can instead use tandem solar cells. Tandem cells are made of multiple p-n junctions made of several different materials. Each material has its own bandgap and can absorb only a limited range of wavelengths of the solar spectrum. Indeed, too far below the bandgap, the efficiency decreases because of considerable heat losses and above the bandgap, photons cannot be absorbed at all. By combining these different materials together, we can then absorb a wider range of wavelengths, which in turns increases the efficiency of the solar cell.
The efficiency can also be improved by using concentrated solar power. Indeed, in their models, Shockley and Queisser only considered illumination swith a non-concentrated sunlight. This means that by using lenses, mirrors or any other concentrated solar power systems, we can reach higher efficiencies by focusing the sunlight on the cell.
These are only two possibilities to exceed the theoretical limit but of course, many other techniques are possible : photon upconversion, intermediate band photovoltaics, etc. However, this out of the scope of our project and thus, will not be further expanded upon.